 コラッツ予想
コラッツ予想 タイプの変化による縮小と拡大
<以下の証明は、読者の方が”コラッツ予想の証明(再々改訂版)”を読んでいることを前提として進めています。まだ読んでいない方はこちらをお読み下さい。> コラッツ操作を行うたびに最下位桁の数値が変化していく。そして、最下位桁の数によってタイ...
 コラッツ予想
コラッツ予想 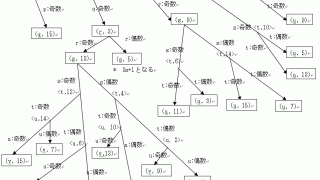 コラッツ予想
コラッツ予想  コラッツ予想
コラッツ予想  コラッツ予想
コラッツ予想  コラッツ予想
コラッツ予想  コラッツ予想
コラッツ予想  コラッツ予想
コラッツ予想  フォニックス<綴りと発音の関係>
フォニックス<綴りと発音の関係>  フォニックス<綴りと発音の関係>
フォニックス<綴りと発音の関係>  フォニックス<綴りと発音の関係>
フォニックス<綴りと発音の関係>